フィルター回路とは目的の周波数を通過させたり減衰させたりするものです。
抵抗、コイル、コンデンサだけで構成するパッシブフィルターでは周波数が低いとコイル等は大きなものになりますが、抵抗とコンデンサ、及び増幅器で構成するアクティブフィルターでは小型に構成可能です。
オペアンプを学ぶうえでアクティブフィルターは克服しておかなければならない応用回路でしょう。
フィルター回路はかなり高度な分野ですが、ここでは最も使われる率が高い、2次と3次のローパスフィルター(LPF)とハイパスフィルター(HPF)に限って定数算出を記述してみます。
2次ローパスフィルター(ハイパスフィルター)とは、カットオフ周波数fcより高い周波数(低い周波数)を12dB/octのカーブで減衰させるものです。
3次ローパスフィルター(ハイパスフィルター)とは、カットオフ周波数fcより高い周波数(低い周波数)を18dB/octのカーブで減衰させるものです。
12dB/oct(12テシベルパーオクターブ)のカーブとは、1オクターブ(周波数にして2倍)の変化で12dBの変化量となります。
18dB/oct(12テシベルパーオクターブ)のカーブとは、1オクターブ(周波数にして2倍)の変化で18dBの変化量となります。
次数が高いフィルターになると急峻な特性となりますが高度な回路になります。
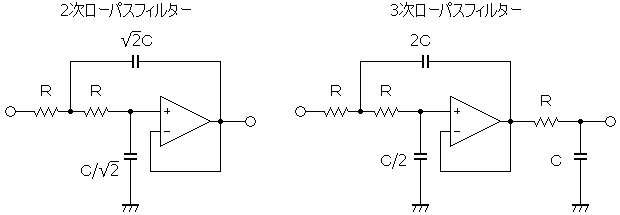
下図は2次ローパスフィルター、3次ローパスフィルターの基本的な回路です。

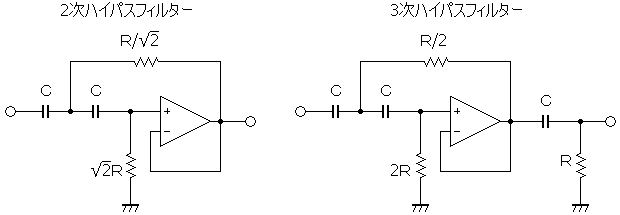
下図は2次ハイパスフィルター、3次ハイパスフィルターの基本的な回路です。
上図ローパスフィルター、ハイパスフィルター共にカットオフ周波数fcは次式で求めます。
カットオフ周波数fc=1/2πCR 〔Hz〕
Rは、数KΩ〜数10KΩの範囲でいいでしょう。
フィルター回路だけを使った製品としてはチャンネルデバイダーが挙げられますね。